Reconstruction of Hyperspectral Imagery from Random Projections using Multihypothesis Prediction

C. Chen, W. Li, E. W. Tramel, & J. E. Fowler

• Link
• PDF
• Code

Astract

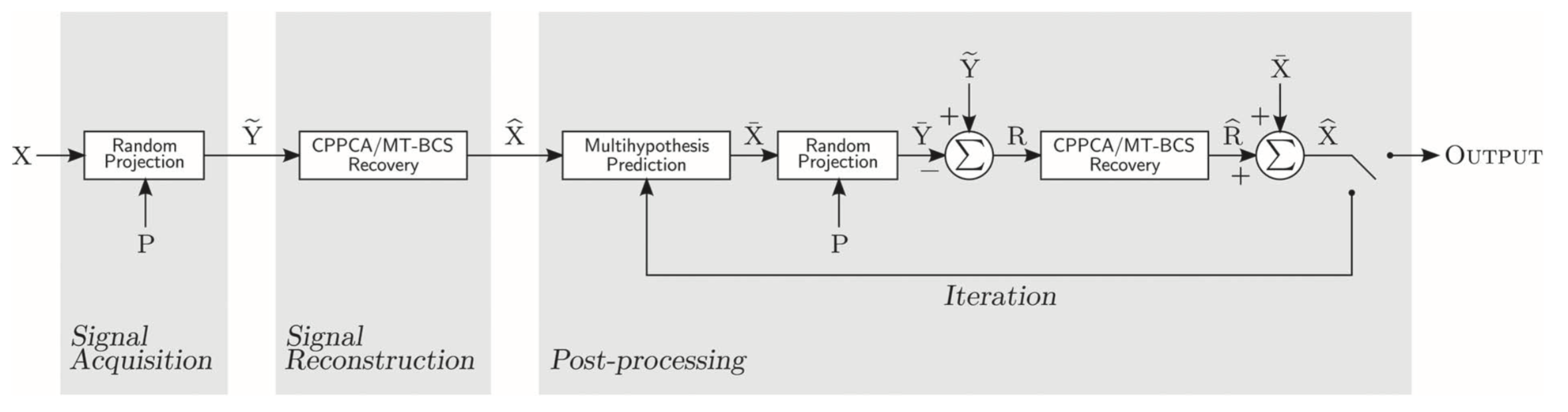
Reconstruction of hyperspectral imagery from spectral random projections is considered. Specifically, multiple predictions drawn for a pixel vector of interest are made from spatially neighboring pixel vectors within an initial non-predicted reconstruction. A two-phase hypothesis-generation procedure based on partitioning and merging of spectral bands according to the correlation coefficients between bands is proposed to fine-tune the hypotheses. The resulting prediction is used to generate a residual in the projection domain. This residual being typically more compressible than the original pixel vector leads to improved reconstruction quality. To appropriately weight the hypothesis predictions, a distance-weighted Tikhonov regularization to an ill-posed least-squares optimization is proposed. Experimental results demonstrate that the proposed reconstruction significantly outperforms alternative strategies not employing multihypothesis prediction.

BibTeX

    article{clt2014,
    Author = {Chen Chen and Wei Li and Eric W. Tramel and James E. Fowler},
    Journal = {IEEE Transactions on Geoscience and Remote Sensing},
    Number = {1},
    Pages = {365-374},
    Title = {Reconstruction of Hyperspectral Imagery from Random Projections using Multihypothesis Prediction},
    Volume = {52},
    Year = {2014}}