Nearest Regularized Subspace for Hyperspectral Classification

W. Li, E. W. Tramel, S. Prasad, & J. E. Fowler

• Link
• PDF
• Code

Astract

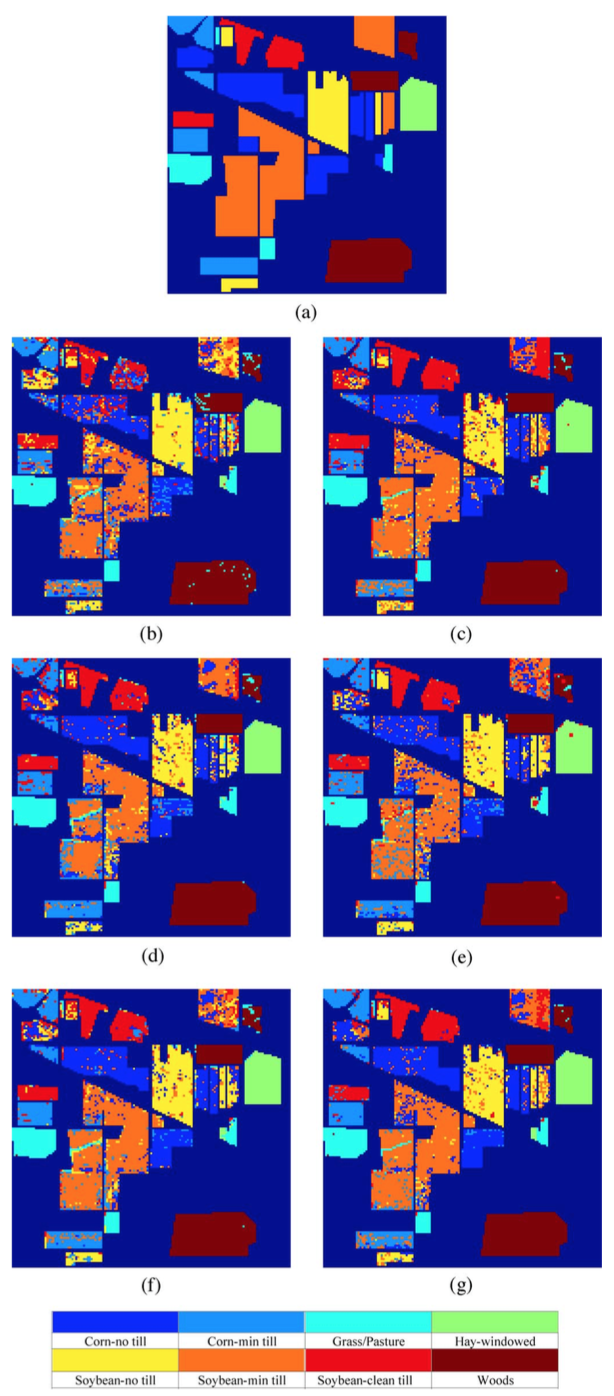
A classifier that couples nearest-subspace classification with a distance-weighted Tikhonov regularization is proposed for hyperspectral imagery. The resulting nearest-regularized-subspace classifier seeks an approximation of each testing sample via a linear combination of training samples within each class. The class label is then derived according to the class which best approximates the test sample. The distance-weighted Tikhonov regularization is then modified by measuring distance within a locality-preserving lower-dimensional subspace. Furthermore, a competitive process among the classes is proposed to simplify parameter tuning. Classification results for several hyperspectral image data sets demonstrate superior performance of the proposed approach when compared to other, more traditional classification techniques.

BibTeX

    article{ltp2013,
    Author = {Wei Li and Eric W. Tramel and Saurabh Prasad and James E. Fowler},
    Journal = {IEEE Transactions on Geoscience and Remote Sensing},
    Number = {1},
    Pages = {477-489},
    Title = {Nearest Regularized Subspace for Hyperspectral Classification},
    Volume = {52},
    Year = {2013}}