Sparse Estimation with the Swept Approximated Message-Passing Algorithm

A. Manoel, E. W. Tramel, F. Krzakala, & L. Zdeborová

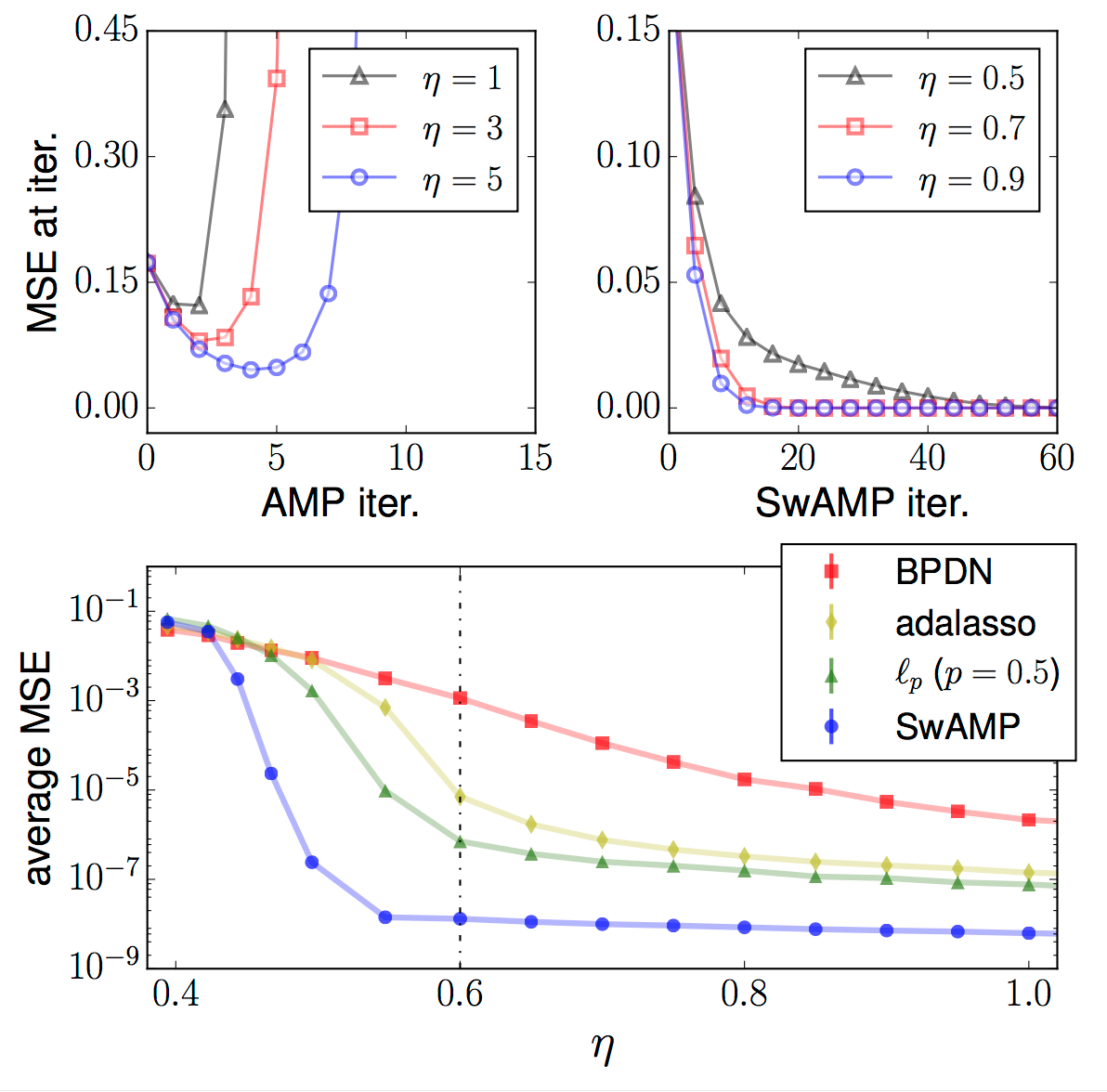
Sparse Estimation with the Swept Approximated Message-Passing Algorithm
At the top, convergence behavior of AMP and SwAMP are compared for CS signal reconstruction for correlated sensing matrices on sparse signals of size \(N = 10^4\) and sparsity \(\rho = 0.2\) with noise variance \(\Delta = 10^{−8}\). The projec- tors have been created according to (30) and are rank-deficient for \(\eta < \alpha = 0.6\). At the bottom, a comparison between log- scale average reconstruction MSE obtained by SwAMP , BPDN, adaptive Lasso, and \(\ell_p\) regularization is given for signals of size \(N = 1024\) for \(\Delta=10−8\), \(\rho=0.2\),and \(\alpha=0.6\).

Astract

Approximate Message Passing (AMP) has been shown to be a superior method for inference problems, such as the recovery of signals from sets of noisy, lower-dimensionality measurements, both in terms of reconstruction accuracy and in computational efficiency. However, AMP suffers from serious convergence issues in contexts that do not exactly match its assumptions. We propose a new approach to stabilizing AMP in these contexts by applying AMP updates to individual coefficients rather than in parallel. Our results show that this change to the AMP iteration can provide expected, but hitherto unobtainable, performance for problems on which the standard AMP iteration diverges. Additionally, we find that the computational costs of this *swept* coefficient update scheme is not unduly burden- some, allowing it to be applied efficiently to signals of large dimensionality.

BibTeX

    conference{mtk2015,
    Address = {Lille, France},
    Author = {Andre Manoel and Eric W. Tramel and Florent Krzakala and Lenka Zdeborov\'{a}},
    Booktitle = {Proc. Int. Conf. on Machine Learning (ICML)},
    Month = {July},
    Title = {Sparse Estimation with the Swept Approximated Message-Passing Algorithm},
    Year = {2015}}

Related Posts

rss facebook twitter github gitlab youtube mail spotify lastfm instagram linkedin google google-plus pinterest medium googlescholar cv vimeo stackoverflow reddit quora quora