Deterministic and Generalized Framework for Unsupervised Learning with Restricted Boltzmann Machines
E. W. Tramel, M. Gabrié, A. Manoel, F. Caltagirone, F. Krzakala
Astract
Restricted Boltzmann machines (RBMs) are energy-based neural networks which are commonly used as the building blocks for deep-architecture neural architectures. In this work, we derive a deterministic framework for the training, evaluation, and use of RBMs based upon the Thouless-Anderson-Palmer (TAP) mean-field approximation of widely connected systems with weak interactions coming from spin-glass theory. While the TAP approach has been extensively studied for fully visible binary spin systems, our construction is generalized to latent-variable models, as well as to arbitrarily distributed real-valued spin systems with bounded support. In our numerical experiments, we demonstrate the effective deterministic training of our proposed models and are able to show interesting features of unsupervised learning which could not be directly observed with sampling. Additionally, we demonstrate how to utilize our TAP-based framework for leveraging trained RBMs as joint priors in denoising problems.
Popular Summary
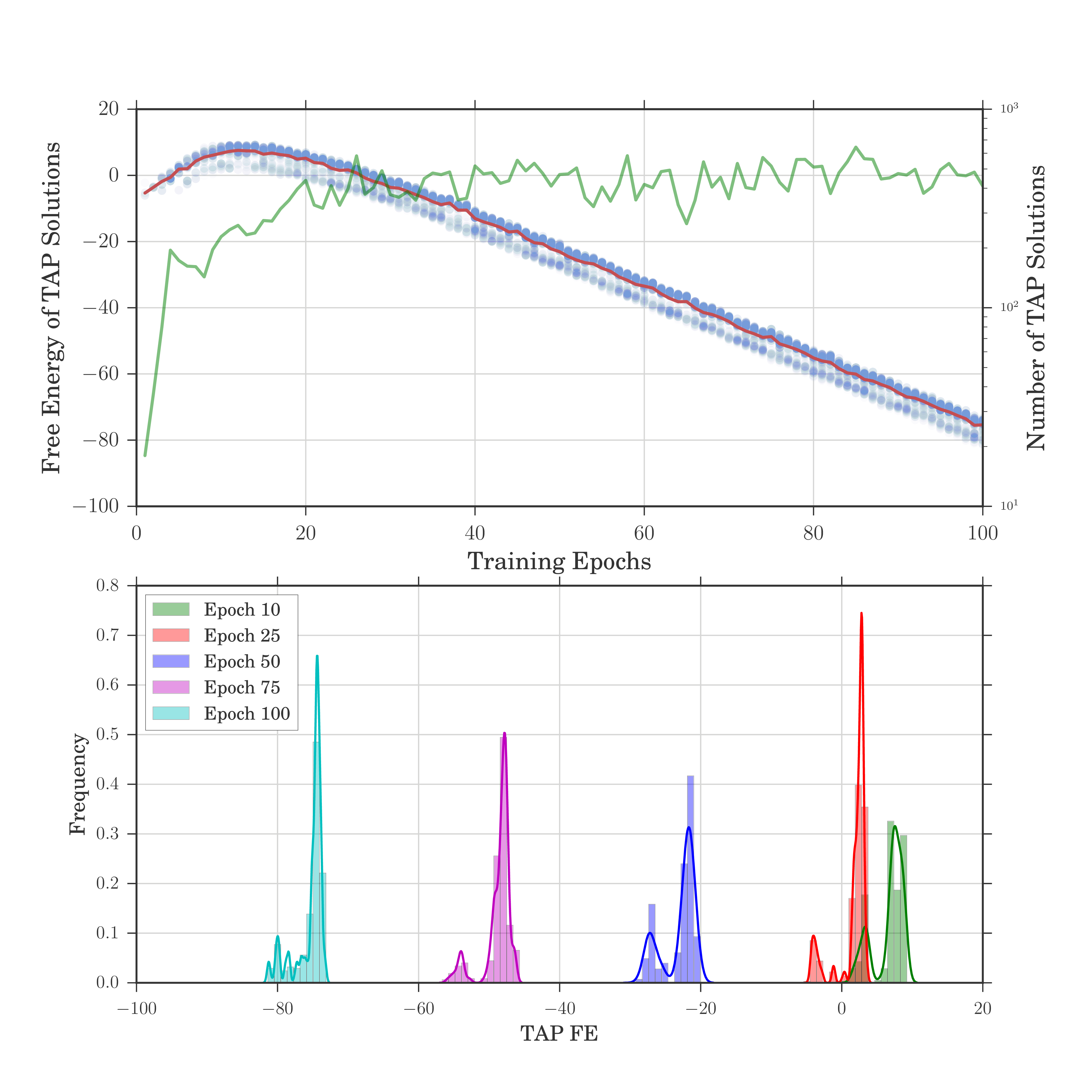
Is it possible to build a machine that teaches itself? How can we grade its proficiency in a learned task? Is it possible to observe what the machine has learned? These are just a few of the open questions in the field of unsupervised machine learning. To help address these questions, we have developed a framework for training, comparing, and analyzing restricted Boltzmann machines (RBMs), an important practical and theoretical building block for deep neural networks.
An RBM “learns” by employing a joint statistical neural model trained to maximize the correlation between data, external observables, and a set of parameters from which it builds internal representations of those observables. Our framework relies on statistical physics methods as a basis for investigating statistical inference over many interacting variables, a common feature of machine learning models. Specifically, we use the Thouless-Anderson-Palmer formalism from spin-glass theory to approximate the macroscopic behavior of the many simple, widely interacting neurons that comprise an RBM.
In our numerical experiments, we demonstrate the effective deterministic training of our proposed models and show interesting features of unsupervised learning that could not be directly observed with sampling. We also show how to use our framework to put RBMs to work on more practical tasks, such as cleaning up noisy signals.
The framework we propose is not only useful for the analysis and inspection of restricted Boltzmann machines, but it also leads to novel practical training techniques and new applications for these unsupervised models.
BibTeX
@article{TGM2018,
title = {Deterministic and Generalized Framework for Unsupervised Learning with Restricted Boltzmann Machines},
author = {Tramel, Eric W. and Gabri\'e, Marylou and Manoel, Andre and Caltagirone, Francesco and Krzakala, Florent},
journal = {Phys. Rev. X},
volume = {8},
issue = {4},
pages = {041006},
numpages = {29},
year = {2018},
month = {Oct},
publisher = {American Physical Society},
doi = {10.1103/PhysRevX.8.041006},
url = {https://link.aps.org/doi/10.1103/PhysRevX.8.041006}}