Belief Propagation & Approximations: Discrete Tomography
E. W. Tramel
Astract
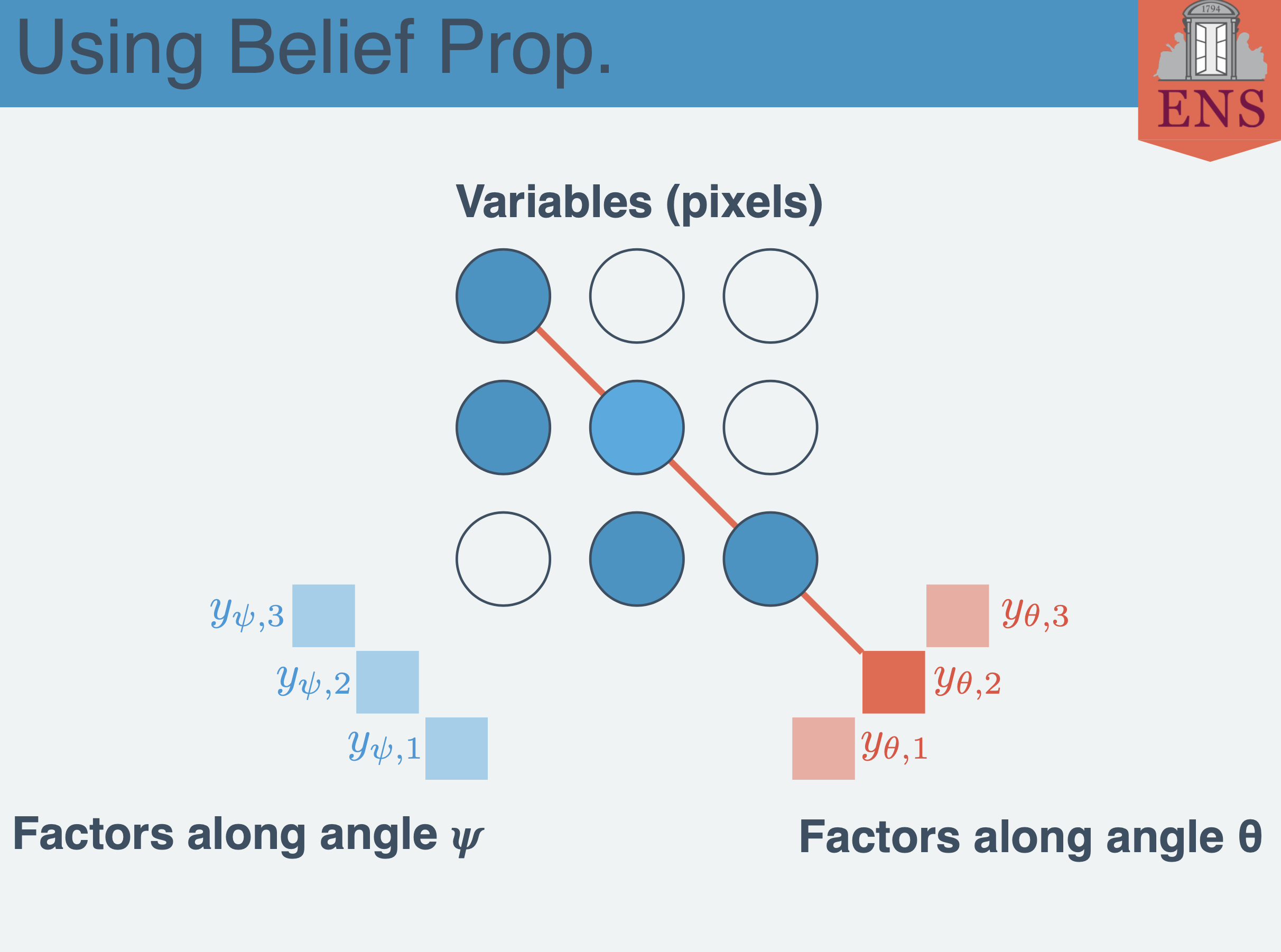
Discrete tomography, or the reconstruction of binary images from a set of limited angular measurements, has applications within many practical and theoretical fields. The binary limitation on pixel values should allow for exact reconstruction from very few measurements, however, developing algorithms to deliver on this theoretical promise is challenging. The field of statistical physics has long been interested in the properties of correlated binary models, e.g. the well-known Ising model, which can be used to capture the intricacies of local correlations within an image. Using these well-known models and approaches can deliver accurate and efficient tomographic reconstruction without yielding to greedy or convex-ified algorithms by instead operating on a grounded statistical interpretation of the problem via the factorized estimation of the a posteriori probability of pixel values. In this talk we will discuss recently published work in applying Belief Propagation (BP) to estimate this factorization, its exact nature in 1D line reconstruction, its advantages over convex techniques such as Total Variation (TV), and the challenges in its application to 2D image models. Next, we will discuss new results which improve on the BP approach both in terms of computational efficiency and accuracy by moving to a 2D model and applying a mean-field approximation with 2nd order corrections (à la Thouless-Anderson-Palmer). Finally, we will discuss some future promising work in the application of these techniques to multi-color discrete tomography problems via the Potts model and its applications to angle-limited electron tomography.