Discrete Reconstruction for Electron Tomography
E. W. Tramel
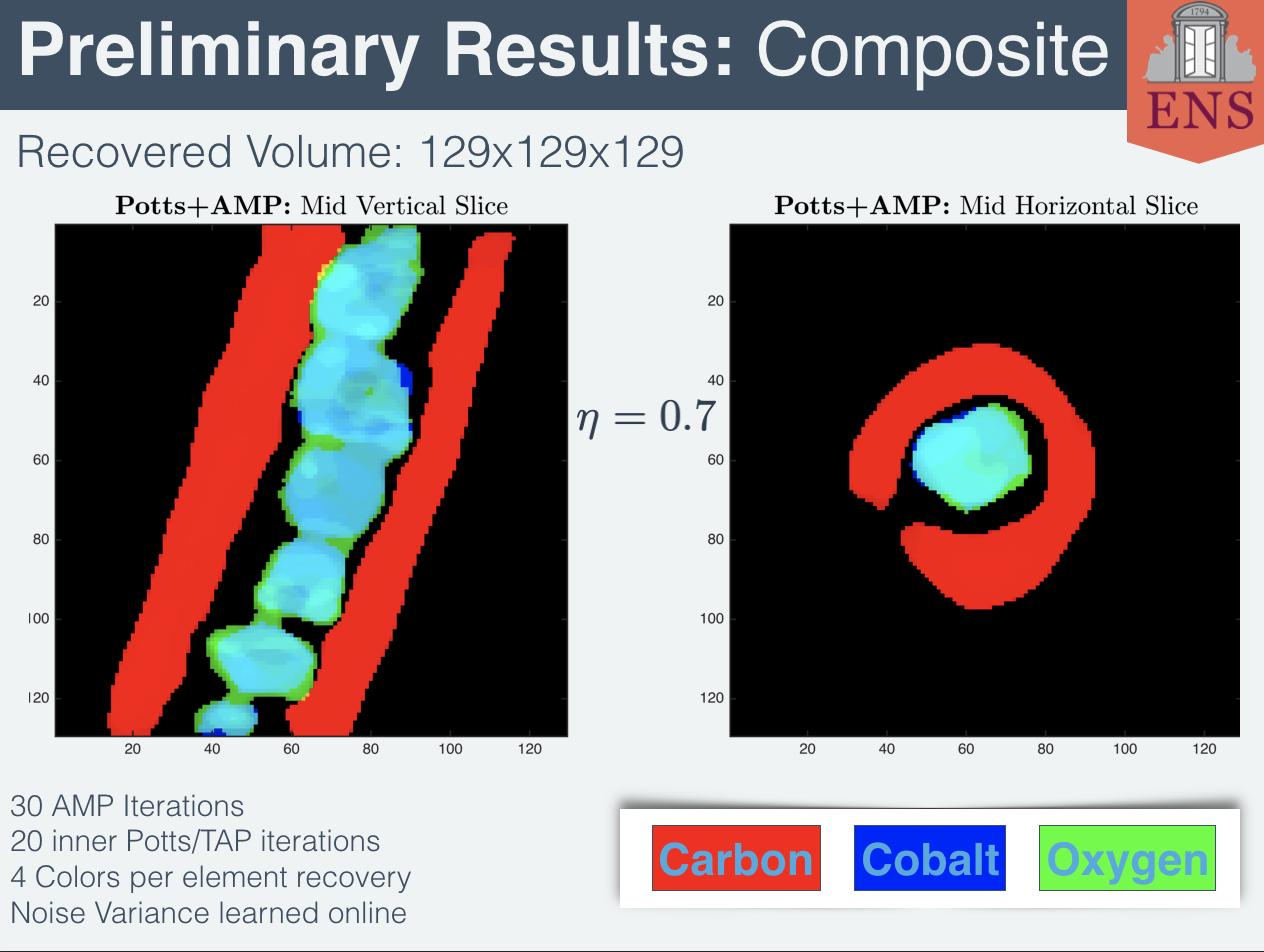
Astract
Discrete tomography, or the reconstruction of binary images from a set of limited angular measurements, has applications within many practical and theoretical fields. The binary limitation on pixel values should allow for exact reconstruction from very few measurements, however, developing algorithms to deliver on this theoretical promise is challenging. The field of statistical physics has long been interested in the properties of correlated binary models, e.g. the well-known Ising model, which can be used to capture the intricacies of local correlations within an image or volume. Using these well-known models and approaches can deliver accurate and efficient tomographic reconstruction without yielding to greedy or convexified algorithms by instead operating on a grounded statistical interpretation of the problem via the factorized estimation of the a posteriori probability of pixel values. We will discuss the application of Belief Propagation (BP) to estimate this factorization, as well as new developments which improve upon the computational efficiency of BP via a second-order mean-field approximation, specifically, the Thouless-Anderson- Palmer approach of statistical mechanics. Finally, we will compare the usefulness of this approach as well as convex techniques, such as Total Variation (TV), for the reconstruction of limited-angle electron tomographic data, investigating the border between discrete and continuous representations.